Вот мы наконец и добрались до этого метода. Литературы по этой технике — целая куча, но как обычно смысл ускользает. Само описание MUSIC достаточно простое: это поиск экстремума произведения двух матриц. Однако что происходит внутри этих матриц — с этим нам предстоит разобраться.
Эту тему довольно сложно понять с нуля, не имея относительно прочной опоры в линейной алгебре. Поэтому нам понадобится аэродром подскока — пара статей, которые я написал ранее: собственные числа и векторы в поиске закономерностей. Метод главных компонент и ковариационная матрица и линейная трансформация. Прочитайте их еще раз, и мы детально, шаг за шагом совершим увлекательное путешествие по пространствам (в буквальном, математическом смысле), а путеводителем для нас будут собственные числа и векторы матриц, которые описывают преобразования этих пространств. Как обычно, ассистировать нам будет Python: строгая нотация языка программирования не допустит никакой двусмысленности, особенно в описании структуры и размерности матриц, чем частенько грешат различные статьи.
Будем рассматривать один частный случай — пример входного сигнала для алгоритма, и на основе этого случая будем делать обобщения на все возможные случаи. За доказательством справедливости этих обобщений отсылаем дотошных читателей к многочисленной литературе; здесь во главу угла поставлена простота и доходчивость изложения.
Компактный симпатичный спектр из двух частот
Зададим исходные данные. Будем иметь дело с сигналом, состоящим из двух частот; также подмешаем немного шума, для реальности происходящего:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# импортируем то что необходимо import numpy as np import scipy.linalg as LA # количество выборок сигнала N = 8 m = np.arange(N) # количество полезных сигналов P = 2 # матрица сигналов x = np.zeros((N, P+1), dtype='complex') # первый сигнал: частота f=3 x[:,0] = 1.0*np.exp(1j*3.0*2.0*np.pi*m/N) # второй сигнал: частота f=5 x[:,1] = 0.8*np.exp(1j*5.0*2.0*np.pi*m/N) # помеха: белый шум x[:,2] = 0.5*np.random.randn(N) |
На самом деле, мы будем наблюдать смесь этих сигналов, и наша задача — определить какие частоты присутствуют в его спектре. Поэтому наблюдаемый сигнал X будет суммой этих массивов:
|
1 |
X = np.sum(x, axis=1) |
Суммирование идет по выборкам, о чем говорит выбор оси axis=1. Поэтому размерность полученной матрицы будет N x 1.
Как и во многих алгоритмах линейного предсказания, в том числе и в MUSIC, конкретная реализация сигнала не представляет большого интереса. Гораздо более важной и обобщенной характеристикой является корреляционная, а точнее автокорреляционная матрица Rxx, выявляющая внутренние связи во входных данных X:
|
1 2 |
XT = np.mat(LA.toeplitz(X)) Rxx = XT*XT.H |
Update:
Матрица Теплица использована для удобства расчета автокорреляционной матрицы, каждый элемент которой представляет собой dot-продукт сигнала sig и его смещенной копии. Чтобы не делать смещение в цикле, с помощью матрицы Теплица входной сигнал (вектор Nx1) превращается в заготовку — матрицу XT размером NxN, которая уже содержит все допустимые сдвиги сигнала sig от 0 до N-1.
Остается только получить dot продукт этой заготовки обычным выражением dot=XT*XT.H
А теперь — прощай, сигнал X! В нашем алгоритме ты нам больше не понадобишься. Вместо тебя будет работать твоя корреляционная матрица Rxx. Сразу скажу, что быть на сцене ей тоже осталось недолго: после того как мы находим собственные числа en и векторы ev корреляционной матрицы Rxx, она тоже перестает быть нужной:
|
1 |
en, ev = LA.eig(Rxx) |
Гарантирую, что с этого момента вы потеряли нить и вам расхотелось читать дальше ) Поэтому самое время остановиться и понять смысл того, что мы делаем. Тем более что большую часть алгоритма мы уже прошли: осталось фактически только одно последнее действие ) Вот она, обманчивая простота матриц!
Итак, наступил обещанный момент погружения в матричные пространства.
Зачем нужны собственные числа и векторы
Идея метода MUSIC состоит в разделении пространства входных сигналов на сигнальную часть и помеховую. Для пространства сигналов существует свой базис, в котором может быть разложена корреляционная матрица Rxx. Поскольку Rxx является самосопряженной (сравниваем Rxx и Rxx.H в Питоне — это одно и то же), то базис разложения будет ортогональным и будет представлять из себя не что иное, как собственные векторы матрицы, масштабированные собственными числами. Что такое ортогональное разложение вы конечно же помните из школьной геометрии, когда рисовали проекции вектора на ортогональные оси x и y. Только это было двумерное пространство, которое легко представить геометрически, а в нашем случае размерности пространства N только и остается, что положиться на формулы.
Проверим, соответствует ли Rxx разложение по ортогональному базису:
|
1 2 3 |
EV = np.mat(ev) EN = np.mat(np.diag(en)).T print(EV*EN.H*EV.H) |
результат будет соответствовать Rxx.
Теперь мы можем предположить, что одна часть собственных векторов, участвующих в разложении Rxx, соответствует сигналу, а другая часть — помехе. Будем также держаться предположения, что полезных сигналов — P, а все остальное в количестве N-P это помехи или шум. Наше предположение некоторым образом подтвердят собственные числа, если мы расставим их в порядке убывания:
|
1 2 3 4 5 6 7 |
idx = en.argsort()[::-1] en = en[idx] # поскольку мнимая часть исчезающе мала, выводим только действительную print(en.real) [ 75.69 50.4 10.39 2.6 1.73 1.69 1.58 0.34] |
По собственным числам можно судить об уровне входных сигналов: как и ожидалось, первые P=2 это полезный гармонический сигнал, остальное — это помеха. Не откладывая на потом, сразу упорядочим и собственные векторы, чтобы они соответствовали собственным числам, расположенным по убыванию:
|
1 |
ev = ev[:,idx] |
Теперь выстраиваем следующую логическую цепочку. Начало ей положит тот факт, что собственные векторы сигнала и помехи — взаимно ортогональны:
|
1 2 3 4 5 6 7 8 |
# пространство помехи: собственные векторы от P и выше EV = np.mat(ev[:,P:]).T # пространство сигнала: собственные векторы до P EVSignal = np.mat(ev[:,:P]) # проверка ортогональности print(EV*EVSignal) |
результат — вектор практически близкий к нулю, что и означает ортогональность.
Как следствие, пространства сигнала и помехи тогда тоже будут ортогональными и как результат полезный сигнал будет ортогонален пространству помехи. Или другими словами, проверка разложения сигнала на базис помехи, образованный ее собственными векторами, покажет ноль. В этом и есть суть метода, при этом естественно не зная составляющего сигнала, в методе он подменяется комплексным опорным экспоненциальным вектором, который является функцией частоты. Путем сканирования частоты подбирается такое значение этого вектора, при котором его разложение на базис помехи будет близок к нулю. При этом зафиксированное значение частоты будет соответствовать факту ее присутствия во входном сигнале.
Разложение экспоненциального вектора на базис помехи
Теперь все дело за тем, как правильно записать нотацию искомого разложения. Собственные векторы помехи мы уже выделили раньше: это вектор EV. Вектор комплексных опорных сигналов будет иметь размерность N:
|
1 |
ref = np.zeros(N, dtype=complex) |
Значения частот будем перебирать из диапазона:
|
1 |
f = np.arange(0,10,0.001) |
Абсолютное значение спектра будем находить как модуль разложения REF*EV.H*EV*REF.H.
Тогда полный цикл перебора опорного вектора будет выглядеть так:
|
1 2 3 4 5 6 7 |
for i in range(f.size): ref = np.exp(1j*2.0*np.pi*m*f[i]/N) REF = np.mat(ref) Mult=REF*EV.H*EV*REF.H Mmusic[i]=np.absolute(1/Mult) Mmusic = 10*np.log10(Mmusic/np.max(Mmusic)) |
Для удобства отображения графика, полученные значения масштабируются в логарифмическом масштабе.
Заметим еще раз: в цикле подбирается такое значение частоты, чтобы разложение опорного вектора в базисе помехи было максимально близко нулю. Это будет означать ортогональность по отношению к пространству помехи и как следствие — соответствие текущего опорного вектора одному из сигналов.
P показан на рисунке.
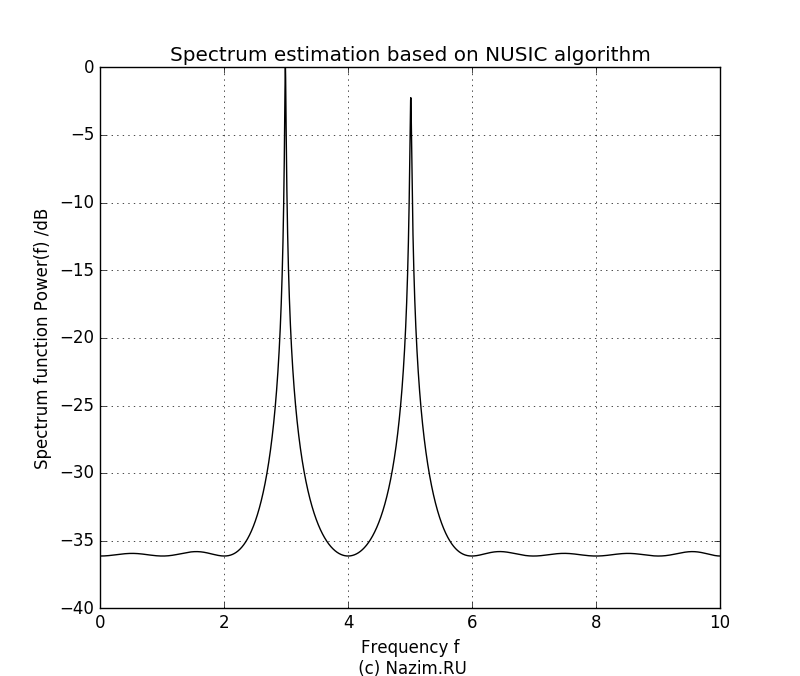
Начнем с P=2:
Здесь неожиданностей нет. На рисунке четко видно два пика относительной частоты 3.0 и 5.0, причем уровень второго сигнала ниже. Мы четко определили наличие двух синусоид в комплексном сигнале в присутствии шума, причем получили значение частот этих сигналов и относительные амплитуды. Теперь возникает интересный вопрос: что произойдет если мы зададим P=1? По идее алгоритм должен посчитать за полезный только один сигнал, а вторую синусоиду вместе с шумом отнести к помехе. Так оно и есть:
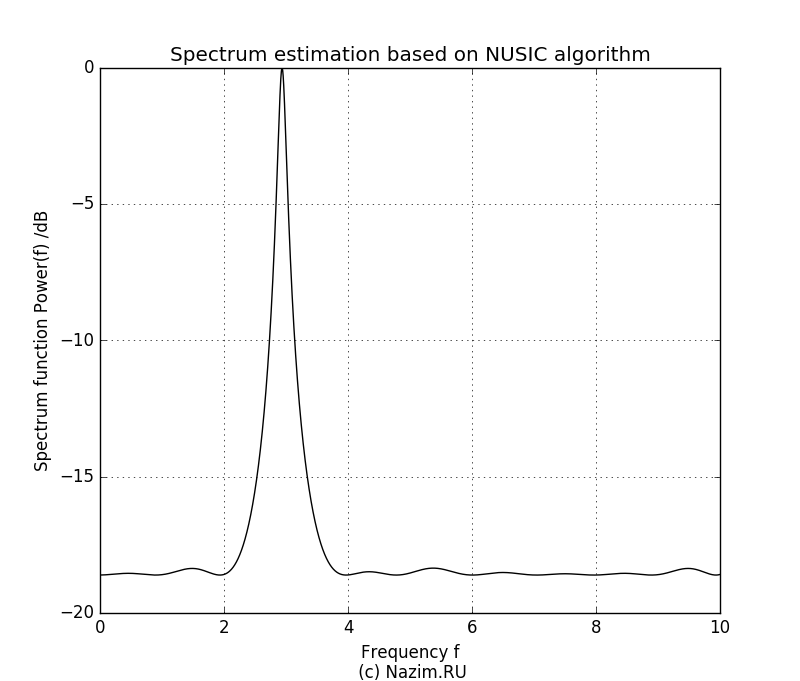
Поскольку амплитуда второго сигнала была ниже, в пищевой цепочке собственных значений он оказался крайним и был подавлен. Остался только сигнал большей амплитуды с частотой 3.0.
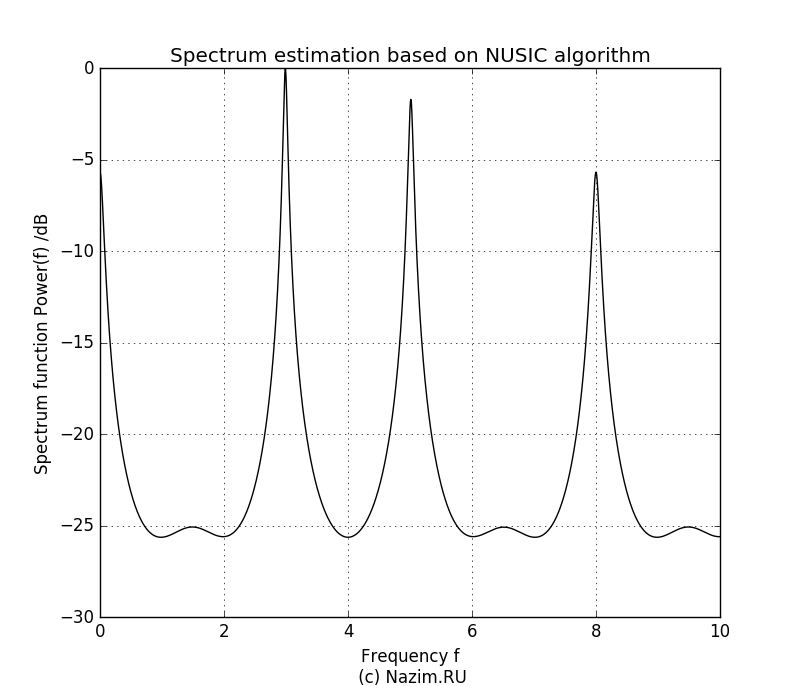
Продолжаем эксперимент. Теперь предположим, что на входе три полезных сигнала, то есть P=3. Что произойдет если белый шум также будет засчитан на равных как нечто полезное?
Получилось довольно неприятно, но не смертельно. Третий всплеск конечно достаточно большой по амплитуде, и такой же всплеск наблюдаем на нулевой частоте. Но мы сами задали шуму приличный уровень — 0.5, так что метод MUSIC довольно лояльно относится к тому, что мы неточно определили количество полезных сигналов.
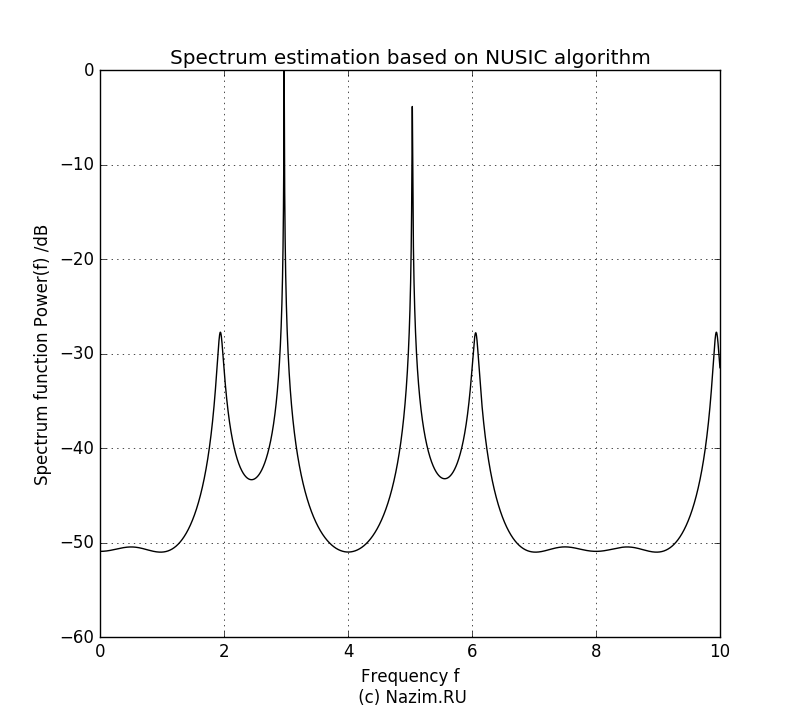
Продолжим расширять наше представление о количестве полезных компонент и зададим P=4:
Как ни странно, картинка стала даже еще лучше. Как и в предыдущих случаях, два полезных сигнала занимают максимум лепестков диаграммы, и хорошо заметно что ошибка в предсказании P дает ее заметное искажение.
Теперь, после того как мы использовали MUSIC для оценки частотного спектра, можно переходить к пространственным частотам — определению направления прихода сигнала, чем мы так любим заниматься в радиопеленгации. Об этом поговорим в следующей статье. И не забывайте что эта тоже была аэродромом подскока!

замечательная статья!
не могли бы Вы пояснить, для чего рассчитывается матрица Теплитца, используемая для расчета корреляционной матрицы?
XT = np.mat(LA.toeplitz(X))
Rxx = XT*XT.H
Когда можно ждать продолжения -> определение направления сигнала.
Заранее спасибо!
Спасибо за оценку статьи.
Матрица Теплица использована только для удобства расчета автокорреляционной матрицы, каждый элемент которой представляет собой dot-продукт сигнала sig и его смещенной копии. Чтобы не делать смещение в цикле, с помощью матрицы Теплица входной сигнал (вектор Nx1) превращается в заготовку — матрицу XT размером NxN, которая уже содержит все допустимые сдвиги сигнала sig от 0 до N-1.
Остается только получить dot продукт этой заготовки обычным выражением dot=XT*XT.H
Дополнил статью этим комментом, действительно из текста неясно, к чему здесь Теплиц )
По направлению сигнала работаем )
Спасибо за статью, очень прошу вас помочь мне. Детально разбираюсь по вашим выкладкам, и все перемоделирую в маткаде, но последний цикл не получантся, так как размерности полученной матрици REF и векторов шумового подпространства EN не совпадают. В результате общее ввражение Mult=REF*EV.H*EV*REF.H не работает. Хотелось узнать, при использовании вектора EN его размерность от P го столбца до N го.
Я тоже сейчас моделирую этот метод, только в c++. У меня получается следующее:
— вектор REF имеет размер N и представляет из себя вектор-строку;
— матрица EV имеет размер (N-P, N), поскольку является транспонированной из последних N-P столбцов матрицы собственных векторов;
— следовательно , выражение Mult=REF*EV.H*EV*REF.H работает.
Но все это не спасает меня, поскольку итоговый спектр у меня получается неправильный ((. Есть подозрение, что где-то вместо операции комплексного сопряжения закралась операция транспонирования.
Да, помню я тоже долго возился с этими размерностями )
Код поменялся, сейчас он выглядит так, я только добавил распечатку размерности матриц:
for i in range(f.size):expo = np.exp(1j*2.0*np.pi*m*f[i]/N)
EXPO = np.mat(expo)
Mult=EXPO*EV.H*EV*EXPO.H
Mmusic[i]=np.absolute(1/Mult)
print(Mult.shape)
print(EXPO.shape)
print(EV.H.shape)
print(EV.shape)
print(EXPO.H.shape)
(1, 1)
(1, 8)
(8, 6)
(6, 8)
(8, 1)
Спасибо за статью! Очень доходчиво.
У меня тоже возникла пара вопросов по реализации:
1) В разложении автокорреляционной матрицы print(EV*EN.T*EV.T) используется транспонированная матрица собственных векторов ( EV.T ). Разве здесь нужно использовать именно транспонированную, а не комплексно-сопряженную ( EV.H )?
2) Аналогично, в проверке ортогональности подпространств сигнала и шума print(EV*EVSignal) используется матрица EV, транспонированная из последних вектор-столбцов матрицы собственных векторов ( EV = np.mat(ev[:,P:]).T ). Разве при проверке ортогональности EV должна быть именно транспонированная, а не комплексно-сопряженная?
Заранее спасибо за ответ!
По вопросам:
1. В вычислении максимума используется комплексно-сопряженная EV.T. Однако, она же должна использоваться при проверке соответствия Rxx ортогональному базису, т.е. правильно будет так:
print(EV*EN.H*EV.H)
Спасибо за замечание, поправил текст. Видимо этот кусок остался от экспериментов с реальными значениями сигналов где EN.T и EN.H одно и то же.
2. При проверке ортогональности используется именно транспонированная матрица (по определению)
Спасибо за оперативный ответ!
Извините за настойчивость, но все-таки не могу понять по второму вопросу. В ортогональном базисе все вектора между собой ортогональны, т.е. скалярное произведение (x, y) = 0. Но скалярное произведение комплексных векторов определяется через комплексное сопряжение (x, y) = SUMM(x_i, y_i.H). Получается, именно по определению EV должна быть комплексно-сопряженная, а не транспонированная, т.е EV = np.mat(ev[:,P:]).H.
Не могло это тоже остаться от экспериментов на действительных данных?
Настойчивость это хорошо, надо же разобраться до конца )
Транспонирование в выражении EV = np.mat(ev[:,P:]).T имеет утилитарный смысл и нужно для выравнивания матрицы EV перед произведением. Мы можем не транспонировать эту матрицу, например написать
EV = np.mat(ev[:,P:])
и тогда нужно будет поменять порядок в произведении EV и EV.H, т.е. формула станет такой:
Mult=REF*EV*EV.H*REF.H
и все будет работать точно также. Может так даже и лучше сделать, чтобы не вносить путаницу с лишним транспонированием )
То о чем Вы говорите в случае произведения комплексных векторов, совершенно правильно: умножать нужно на комплексно-сопряженную транспонированную матрицу. Это и происходит в вышеприведенном выражении в общем произведении при вычислении Mult.
Вопрос к автору статьи, есть ли еще похожие описаниния, других методов?(CAPON, ESPRIT,Барлета, Прони)Буду очень признателен. Автору респект.
Всем привет, в маткаде все собрал, заработало. Но схожесть с рисунками, не однозначная, амплитуда откликов одинаковая, а не разная. Кому интересно могу скинуть прогу. Вопрос к автору статьи, есть ли еще похожие описаниния, других методов?(CAPON, ESPRIT,Барлета, Прони)Буду очень признателен. Автору респект.
Здравствуйте, возникли такие же трудности, не могли бы вы поделиться программой ? Заранее благодарен, надеюсь, что откликнетесь !
Все же, хочу разобраться с амплитудой откликов, графики как у автора но, как бы отражены зеркально. Целый день вожусь, как я думаю дело в упорядочении собственных векторов, согластно индексов упорядоченного по убыванию вектора en.
У меня тоже спектр зеркально отражён :). Я делала четко по вышепредставленному алгоритму. Так что это, получается, не ошибка.
А один пик при Р=1, получается?
Людмила, а вы распологали собственные числа в порядке убывания и после этого столбцы собственных векторов, в соответствии с индыксами этих чисел. В результате получаются два вектора EN.
Не могу получить один пик при Р=1, при Р=3 самый правый пик выше всех, потом идут два пика на частотах 3 и 5 одинаковой амплитуды и самый левый пик выше этих двух. Немогу найти ошибку.
Игорь, у вас моделируются чистые сигналы, без шума? Если так, попробуйте подмешать шумовую составляющую. Без нее получаются неадекватные результаты
Нет с шумом, равномерный шум с СКО 1 помноженный на 0.5. В маткаде, это выглядит так 0.5*rnd(1).Спасибо, что ответили.
У меня при P=1 два пика, и при Р=2 два пика, но более выраженные. Мучаюсь, не получаются такие же графики как в статье.(
Да, конечно. Я сортировала собственные числа в порядке убывания, и собственные вектора в соответствии с этими собственными числами.
При P=1 у меня получается один пик, как и должно быть.
Но в основном я отлаживалась при P=3 и больше. Спектр получается зеркальный относительно 0 (у меня ось x с положительной и отрицательной областями) и пики слегка смещены. Не скажу на сколько в герцах, потому что опорный вектор я выщитываю не совсем от частоты.