Адаптивная фильтрация сигналов сродни магии. И в самом деле, делая самые общие предположения о природе сигнала и помехи, адаптивный фильтр весьма эффективно использует дополнительную информацию о мешающих сигналах — например, о той же самой помехе.
Самая распространенная постановка вопроса в области адаптивных фильтров — это синтез речи, то есть нахождение такой структуры фильтра, которая обеспечит имитацию голосовой структуры человека. Наш контекст совершенно другой: это поиск методов эффективного подавления помехи от базовой станции в когерентной пассивной локации. При этом у нас есть отличный источник информации о помехе: это сигнал с антенны со сформированной прямо на базовую станцию диаграммой, в котором не должен присутствовать полезный, отраженный от цели сигнал.
Хороший пример из медицины
До того как перейти к тому, как адаптивная фильтрация будет использоваться в нашем пассивном радаре, вначале рассмотрим более понятный (и поэтому может быть распространенный) пример из медицины. В этом примере наш адаптивный фильтр пассивного радара, изображенный на рисунке, будет использоваться следующим образом.
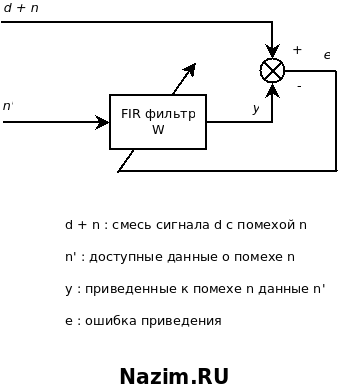
Адаптивный фильтр
Существует известная задача снятия электрокардиограммы, которая формируется на основе электрических сигналов сердечных мышц. Эта задача усложняется, когда необходимо записать сердцебиение у плода беременной женщины. В этом случае ее собственное сердце является источником помехи в записи электрических импульсов сердца ребенка (полезный сигнал), которую можно и необходимо устранить. Задачу подавления этой помехи выполняет наш адаптивный фильтр. В данном конкретном случае, источником дополнительной информации о помехе является второй датчик, который записывает только сигнал сердца матери.
Прямо в этом месте у читателя возникает легкое недоумение. Зачем городить огород с адаптацией, если можно просто вычесть сигнал матери из записи и останется только сигнал ребенка? К сожалению, ничего хорошего из этого не выйдет. Результат будет отвратительным по следующим причинам:
- помеха которую мы наблюдаем в смеси с полезным сигналом не является точной копией помехи которую мы снимаем с источника дополнительной информации; эти сигналы взаимозависимы, коррелированы но не идентичны;
- ситуация непрерывно меняется со временем, внося амплитудные и фазовые искажения.
После этого становится очевидным, что задача, которую решает адаптивный фильтр, следующая: приведение дополнительной информации о помехе к такому виду, чтобы она стала по возможности полностью идентичной самой помехе содержащейся в смеси со входным сигналом, и только после этого выход фильтра можно вычесть из наблюдаемого сигнала. Что приведет к подавлению помехи.
Применительно к нашему примеру, структура адаптивного фильтра описывается следующим образом:
- d + n : смесь искомого сигнала (сигналы сердца ребенка) и помехи (сигналы сердца матери, которые дошли до датчика снимающего сигнал ребенка);
- n’ : дополнительная информация о помехе: сигнал с другого датчика в районе сердца матери; подается на вход фильтра который за счет коэффициентов W подстраивает его под помеху n;
- y : выход фильтра, который по возможности должен как можно точнее совпадать с помехой n в суммарном сигнале d + n;
- e : сигнал ошибки, указывающий на то, насколько наше представление о помехе y разошлось с ее реальным значением n.
Фильтр непрерывно отслеживает сигнал ошибки e, изменяя на его основе свои коэффициенты W для обеспечения лучшей адаптации. Сигнал ошибки e и является результатом всей нашей системы, как бы странно это не звучало. Если бы адаптация прошла идеально, то этот сигнал ошибки и будет представлять собой искомый сигнал d, то есть сигнал сердца плода.
Магия адаптации
Как мы видим из медицинского примера, на самом деле все просто. Надо всего лишь минимизировать ошибку за счет подбора коэффициентов фильтра. Все дело в том, каким образом определить эти коэффициенты.
Не буду углубляться в теорию: она достаточна сложна. Замечу лишь, что существует строгое теоретическое решение, связанное с обращением матриц, и которое совершенно не подходит для реальных средств обработки сигналов. Для реального мира работают итерационные алгоритмы, которые приводят практически к тем же самым результатам. Тех, кто ожидает таинства процедуры нахождения коэффициентов W, ждет глубокое разочарование: они определяются довольно топорным методом как подбираемая экспериментальным способом доля от смеси сигнала ошибки фильтра и сигнала помехи, наблюдаемой на определенном интервале. В этом проблема с адаптивными фильтрами: ускользает физический смысл внутреннего принципа работы. Зато результаты работы вполне можно использовать для своих целей.
Давим FM-станцию в пассивном радаре
Вначале пару слов о том, зачем нужна адаптация в PCL. Основной алгоритм обработки пассивного локатора — это функция неопределенности, уровень боковых лепестков которой сложно сделать меньше чем минус 40 — 50 дБ относительно пика за разумное время. С учетом того, что помеха превышает сигнал на уровни соизмеримые 100 дБ, этого явно недостаточно. Дополнительный (20 — 40 дБ) выигрыш может дать использование направленных свойств антенной системы, что несколько улучшает ситуацию. Но если мы можем получить дополнительную информацию о помехе, то грех не использовать это для адаптивной фильтрации, не правда ли?
По отношению к пассивному радару сигналы адаптивного фильтра приобретают следующий смысл:
- d + n : смесь полезного сигнала отраженного от цели и помехи — сигнала базовой станции;
- n’ : дополнительная информация о помехе: сигнал базовой станции, полученный с антенной системы;
- y : выход фильтра, в котором подавляется помеха;
- e : сигнал ошибки, представляющий собой сигнал d, который не может быть подавлен адаптивным фильтром, поскольку фильтр не получает информацию об этом сигнале.
Теперь пришло время смоделировать поведение адаптивного фильтра. Будем использовать для этой цели Python, поскольку он содержит мощные библиотеки работы с массивами и обработки сигналов. Воспользуемся записью реального сигнала с эфира FM станции Sfile для моделирования поведения адаптивного фильтра, это будет сигнал n. Для получения полезного отраженного сигнала применим к n процедуры временного и частотного сдвига. Питоновская функция target, которая это делает, выглядит следующим образом.
|
1 2 3 4 5 6 7 8 9 10 |
import numpy as np def target(Sfile, count, delay, dopler, Ts): St = Sfile[delay:delay+count] tall = np.linspace(-Ts*count/2., Ts*count/2., count) exf = np.exp(1j * 2. * np.pi * dopler * tall) Stf = St * exf return(Stf) |
Помимо собственно выборки записи FM сигнала Sfile, функция принимает в качестве параметров:
- count : размер выходного сигнала, который нужно сформировать;
- delay : имитируемая задержка;
- dopler : имитируемый доплеровский сдвиг;
- Ts : расстояние между выборками по времени.
Фильтр использует размерность входных выборок nsamples и количество звеньев фильтра taps:
|
1 2 3 4 5 |
for n in np.arange(nsamples): for i in range(0, taps): if n >= i: sOutput[n] = sOutput[n] + w[i] * antFm[n-i] sError[n] = antTarget[n] - sOutput[n] |
Адаптивный фильтр формирует выходной сигнал ошибки sError как разность сигнала цели antTarget, содержащего также помеху, и выход FIR фильтра sOutput. На вход FIR фильтра подается сигнал помехи antFm (выделенный антенной сигнал базовой станции), который суммируется с учетом весовых коэффициентов w.
Здесь видимо уместно сделать следующее замечание: в питоновском коде циклы for оставлены только для наглядности (как и оператор if). На самом деле, возможности обработки массивов библиотеки numpy позволяют обойтись без циклов, что существенно повышает производительность программы.
Фильтр у нас уже есть, дело за правильными коэффициентами w. Вот этот кусочек магии:
|
1 2 3 4 5 |
for i in range(0, taps): if n >= i: w[i] = w[i] + (beta * sError[n].real * antFm[n-i].real) else: w[i] = 0 |
Из этого кода также следует, что изначально значения используемых сигналов — комплексные.
Магический кусочек кода содержит магическую константу beta. Она определяет сходимость фильтра и его быстродействие. Как и все в этом мире, эти два параметра выбираются исходя из компромисса: на сходимость фильтра требуется время, и если его у нас мало, то точность его работы будет хуже.
Как это работает
Теперь все готово для того чтобы запустить нашу адаптивную машину. Все действующие лица и исполнители, то есть сигналы, представлены на рисунке в цвете:
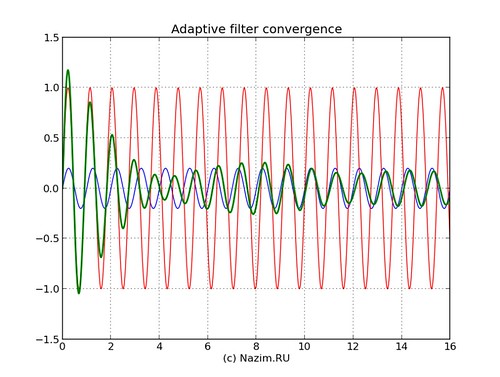
Сходимость адаптивного фильтра
Синим цветом представлен искомый сигнал, красным — помеха. По уровню помеха больше сигнала; сигнал также смещен по частоте относительно помехи (доплеровский сдвиг). Смесь сигнала и помехи подается на вход фильтра; кроме этого модифицированная помеха используется как источник дополнительной информации. Сигнал ошибки, или выход фильтра обозначен зеленым цветом.
Из рисунка следует, что на адаптацию ушло 8 — 10 периодов полезного сигнала. Вначале выход адаптивного фильтра полностью представлен сигналом помехи; дальше, по мере адаптации, помеха давится и выход фильтра соответствует уже искомому полезному сигналу. Также видно, что в установившемся режиме выход фильтра несколько запаздывает относительно полезного сигнала: это связано с фазовой задержкой в FIR фильтре.

А есть какие-то практические примеры? Т.е. вот два АЦП, вот две антенны, одна крутится (сканирует пространство по азимуту), вторая смотрит на базовую станцию, вот плис, вот ПК, вот карта местности с движущимися точками. Или пока только теория? У Вас в железе все получилось? Сам давно хочу потрогать эту тему, но никак не решусь.
На базе этого и других алгоритмов разработан прототип. Содержит два диполя, включенные через диаграммообразующую схему, в результате — сложение в направлении отраженного сигнала синфазно, в направлении FM станции — противофазно. Остаток подавленного сигнала базовой станции используется как опорный канал.
Далее — 2х радиоприемный тракт — разработанные и изготовленные модули RF Frontend, содержащие квадратурный смеситель, каналы ПЧ и единый синтезатор для обеспечения когерентности.
После радио — высокоскоростные платы АЦП FMC140, работающие на частоте 250 mS/s, подключены к плате Zedboard, где на ПЛИС реализован первичный процессор с фильтром и дециматором, а на ARM выполнен алгоритм адаптивного фильтра.
Далее все это идет на платы BeagleBoard, где на ядре DSP считается функция неопределенности. Графика — на лаптопе.
С прототипом ездили в поля, получили много информации, сейчас работаем с этим. Главный результат — большое практическое неудобство использования DSP с целочисленной арифметикой и низкой скоростью. Нужно переходить на современные чипы с плавающей точкой. Ну и есть еще другие вещи.
Работаем, все в процессе )
Более подробное описание составных частей прототипа PCL и фото можно посмотреть здесь:
http://www.primaria.ru/ru/category/pcl