2D Alpha — Beta фильтр в траекторной обработке

Наконец подошло время и для альфа — бета фильтра. Этот фильтр представляет собой более простую реализацию фильтра Калмана и использует два параметра — альфа и бета.

Фактически, эти параметры — весовые коэффициенты к ошибкам прогноза позиционирования и скорости объекта. Альфа и бета остаются постоянными во время работы фильтра и задаются изначально как константы.

Работа 2D фильтра моделировалась в предположении, что движение объекта, или цели в двумерной системе координат является независимым, то есть цель может двигаться совершенно произвольно. Если сделать другое предположение, что движение цели обусловлено, то подозреваю можно улучшить работу фильтра. Некоторые соображения на эту тему я выскажу в конце статьи.

Как работает Альфа — Бета фильтр

Поскольку фильтрация по каждой из осей X, Y происходит независимо, проследим работу фильтра по одной из осей. Для нас важен физический смысл того, что происходит, поскольку математическая реализация фильтра довольно проста и занимает вместе с графикой не больше 100 строк на Питоне.

Итак, цель движется в горизонтальной плоскости, и мы наблюдаем ее положение скажем по оси X. Наблюдение сводится к измерению x координаты цели в каждый дискретный момент времени с равномерными промежутками. Возьмем отдельно взятый отсчет по координате x, допустим пусть это будет 1523 метра. В этот момент альфа — бета фильтр делает предположение, или прогноз, или предсказание о том, где цель очутится в следующий момент времени. Как он это делает?

Предположим, что в тот момент когда мы достигли отсчета 1523м, у нас уже было предсказание, сделанное в предыдущей точке о том, где мы будем находится. Скажем, до текущего отсчета альфа — бета фильтр предсказал нам что наша текущая позиция (а для него тогда это была наша будущая позиция) составит 1535м. Этого для нас, точнее для фильтра достаточно, и теперь внимательно наблюдаем за тем что он будет делать с настоящим и прошлым. Он из этого будет делать будущее.

Во-первых, фильтр тут же узнает о том, насколько он ошибся в своем прошлом прогнозе. Ошибка составит 12м. Фильтр постоянно старается минимизировать эту ошибку и улучшить точность предсказания. Для этого он берет долю альфа от этой ошибки и добавляет эту долю к своему прошлому прогнозу. После добавления это значение становится предсказанием будущего расстояния.

То же самое фильтр проделывает со скоростью движения, только для корректировки скорости используется параметр бета. Прогноз скорости также используется для определения будущего расстояния, поскольку цель проходит его за промежуток между двумя отсчетами.

Предсказание положения цели и траекторная обработка

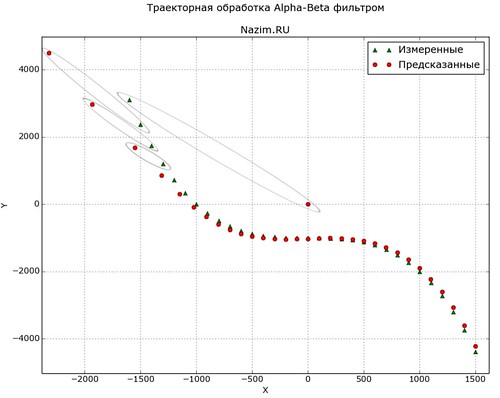
Обратимся к диаграмме в начале статьи. На ней показаны результаты моделирования движения цели в горизонтальной плоскости. Альфа — бета фильтр использовался в двух каналах X, Y независимо. Измеренные, или реальные положения цели обозначены зелеными треугольниками, а предсказанные фильтром положения цели — красными кружочками. Цель движется с левого верхнего угла к правому нижнему углу диаграммы.

Поскольку в начале работы альфа — бета фильтра предыдущее положение цели неизвестно, ее координаты задаются нулевыми. Соответственно, с самого начала работы фильтра возникает максимальная ошибка, которую обозначает самый большой эллипс на рисунке. Эта ошибка — разница между текущим положением цели и нулевой координатой. На втором шаге фильтр уже существенно улучшает прогноз и ставит его в левую верхнюю часть диаграммы, но ошибка обозначенная эллипсом поменьше по прежнему высока. Видно, как за первые четыре итерации значения ошибок неуклонно снижаются и к началу выхода траектории цели на движение вдоль оси X фильтр предсказывает будущее значение красным кружком практически там же, где будет находиться цель. По мере дальнейшего движения цели и роста крутизны маневра, начинает наблюдаться отставание предсказанного значения от реального. Для того чтобы сократить это отставание, фильтру не хватает работы по второй производной движения — по ускорению. Ускорение учитывается в более сложном альфа — бета — гамма фильтре, где параметр гамма определяет вклад ускорения цели в предсказание положения.

На основе предсказания строится траекторная обработка. Цель такой обработки — логически связать вместе все отсчеты (plots) и назначить их принадлежащему одному треку цели (track). Если каждый плот попадает в предсказанную область, то его с высокой степенью вероятности можно считать принадлежащему этому треку.

Зависимое по координатам движение

Как я заметил выше, X и Y каналы фильтра работают независимо друг от друга. Это значит, что погрешность предсказания, полученная в одном канале, никак не учитывается в другом. Однако, если мы сделаем дополнительные предположения о характере движения цели, мы можем сделать каналы зависимыми и улучшить точность предсказания. Одно из таких предположений может заключаться в следующем. Допустим, цель совершает маневр — движение по кругу. Сразу в двух каналах возникает ошибка предсказания, которая будет полностью скомпенсирована в альфа — бета фильтре только после выхода на прямолинейную траекторию движения. Однако, если мы введем зависимый параметр — длину вектора, ортогональные составляющие которого образованы ошибкой в каждом из каналов, и убедимся в том что длина вектора неизменна (цель сохраняет скорость и только поворачивает), то мы можем обеспечить дополнительную компенсацию ошибки. Такая межканальная компенсация может заключаться в следующем: очевидно, что при повороте цели ошибка в каналах будет расти, но с разными знаками. Вводя дополнительные коэффициенты, можно создать упреждающее предсказание, основанное на предположении о маневре цели.

В общем надо бы попробовать это сделать и сравнить с обычным альфа — бета фильтром )