Задачи распознавания изображений обладают интересным свойством. Вот смотришь на картинку и видишь прямую, которая образована разбросанными точками. Как только пытаешься получить эту прямую по данным точек в программе — сразу возникают алгоритмические трудности.
Что поделаешь, это еще одно напоминание о том, что человеческий глаз — это совершенное средство обработки данных.
В этом примере прямая — это некоторая закономерность, которую нужно найти в потоке данных. Где может пригодиться такой алгоритм? Например, в распознавании маркеров взлетно — посадочной полосы оптической системы посадки БПЛА. Или хотя бы определить направление, в котором дедушка Ляо идет из кабачка домой.
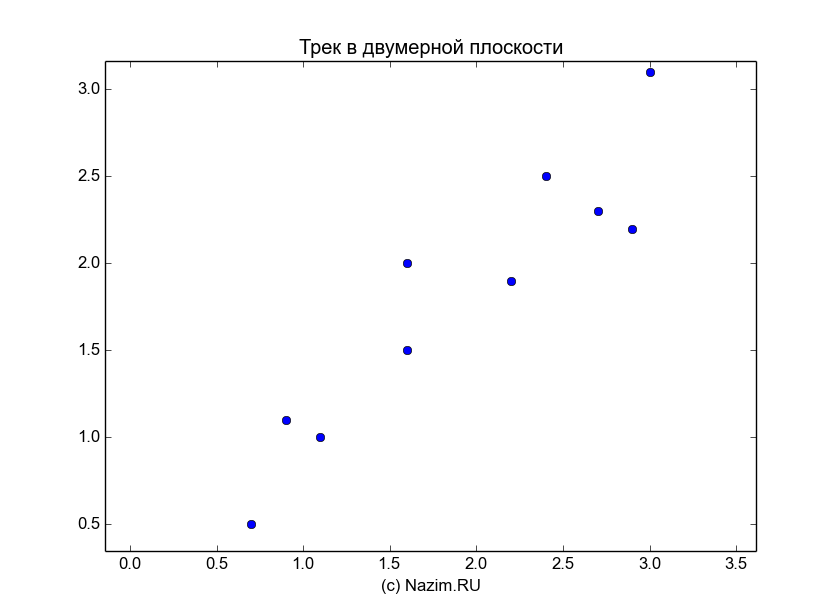
Понаблюдаем же за дедушкой Ляо. Хорошо посидев с друзьями своей юности в кабачке, он спешит к домашнему очагу. Как видно из карты перемещений, у дедушки Ляо не очень уверенная походка. Тем не менее, очевидно что он стойко идет к своей цели. Очевидно для нас, потому что мы пользуемся совершенными инструментами — собственными глазами. А что делать компьютеру? Как ему выявить закономерность на основе данных десяти точек?
Для этого можно использовать понятие собственных чисел и собственных векторов матрицы. Поскольку теорию мало кто любит и тем более мало кто запоминает, рассмотрим эти понятия на простом примере и затем вернемся к дедушке Ляо во всеоружии.
Матрицы линейного преобразования: портим фигуру
По старой доброй традиции, воспользуемся богатыми математическими возможностями Питона. Не мудрствуя лукаво, нарисуем следующую фигурку — двойной ромбик:
|
1 2 |
tst = np.mat([ [-3,-2,-2,-1,-1,0,0,1,1,2,2,3], [0,-1,2,-2,4,-3,6,-2,4,-1,2,0] ]) |
Для наглядности можно вывести значение этой матрицы на экран:
|
1 2 |
[[-3 -2 -2 -1 -1 0 0 1 1 2 2 3] [ 0 -1 2 -2 4 -3 6 -2 4 -1 2 0]] |
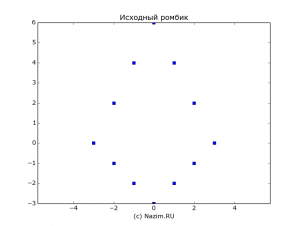
Матрица определяет фигурку из 12 точек, первая строка — x координаты точек, вторая строка — y координаты. Выглядит фигурка так:
На этом с исходными данными все. Теперь начинается самое интересное: мы будем портить нашу фигурку. Для этого матрицу фигурки умножаем на матрицу линейного преобразования A, которая может растягивать фигурку по горизонтали:
|
1 |
A = np.mat([[2,0],[0,1]]) |
Или сжимать также по горизонтали:
|
1 |
A = np.mat([[0.5,0],[0,1]]) |
Растягивать по вертикали:
|
1 |
A = np.mat([[1,0],[0,2]]) |
Перекос:
|
1 |
A = np.mat([[1,1],[0,1]]) |
Мы можем даже повернуть фигурку, например на 30° по часовой стрелке. Как вы догадываетесь по значению элементов матрицы линейного преобразования, не обошлось без синусов и косинусов соответствующего угла поворота:
|
1 2 3 |
A = [[ 0.87 0.5 ] [-0.5 0.87]] |
Или вообще вместе со сжатием и растяжением еще перекосить ее так, что сразу и не узнаешь:
|
1 |
A = np.mat([[1.2,0.5],[0.2,1.2]]) |
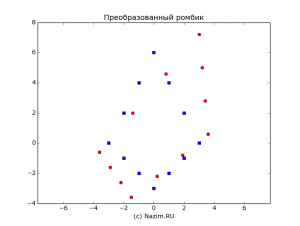
Воспользуемся последним преобразованием и скособочим нашу фигурку:
|
1 2 3 |
TST = A*tst [[-3.6 -2.9 -1.4 -2.2 0.8 -1.5 3. 0.2 3.2 1.9 3.4 3.6] [-0.6 -1.6 2. -2.6 4.6 -3.6 7.2 -2.2 5. -0.8 2.8 0.6]] |
Матрица линейного преобразования A перевела 12 наших исходных векторов на другие позиции, то есть поменяла их координаты: на то оно и преобразование.
Однако, существуют такие векторы, которые напрочь отказываются преобразовываться. При попытке матрицы линейного преобразования сжать их, растянуть, перекосить или повернуть они переходят сами в себя. Для каждого линейного преобразования эти векторы свои, поэтому они называются собственными векторами матрицы. Есть еще и собственные числа, которые участвуют во всем этом следующим образом: эффект от линейного преобразования собственного вектора такой же, как будто бы его просто умножили на собственное число. Проще говоря, собственное число — просто масштабирующий множитель. Матрице конечно обидно, что она ничего не может сделать с собственным вектором и ее многомерный эффект преобразования сводится к простому умножению на число. Но что поделать!
Вскрытие собственников
Найдем собственные числа и собственные векторы нашей матрицы преобразования A. На Питоне это делается одной строчкой:
|
1 |
w, v = np.linalg.eig(A) |
Я придерживаюсь обозначений, которые показаны в примерах модуля numpy Питона: w — это собственное число, v — собственный вектор. Неудобно, что слова vector и value начинаются на одну и ту же букву, и поскольку вектор главнее, собственное число получило наименование w.
Посмотрим что получилось:
|
1 2 3 4 5 6 7 8 |
A = [[ 1.2 0.5] [ 0.2 1.2]] v = [[ 0.85 -0.85] [ 0.53 0.53]] w = [ 1.52 0.88] |
Очевидно, что для нашей матрицы линейного преобразования существуют два собственных вектора и два собственных числа.
Первая парочка:
|
1 2 3 4 5 |
v1 = [[ 0.85] [ 0.53]] w1 = 1.52 |
Наступил момент истины. Подвергнем вектор линейному преобразованию:
|
1 2 3 4 5 6 |
A*v1 = [[ 1.28] [ 0.81]] w1*v1 = [[ 1.28] [ 0.81]] |
Так оно и есть: собственный вектор «не чувствует» родную матрицу A и остается таким же, как и был, точнее — умноженным на собственное число.
Проверка второй парочки:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
v2 = [[-0.85] [ 0.53]] w2 = 0.88 A*v2 = [[-0.75] [ 0.47]] w2*v2 = [[-0.75] [ 0.47]] |
Тоже самое: какого-либо желания трансформироваться не обнаружено напрочь.
Principal Component Analysis (PCA), или Метод главных компонент в поисках закономерностей
Теперь мы хорошо подготовлены к тому, чтобы переварить идею метода PCA, вынесенного в заголовок. Метод основан на поиске осей максимальных изменений входных данных; эти оси называются компонентами, что и послужило основой для названия метода. Подробное и самое главное — понятное описание метода для химических приложений изложено здесь (вспоминая замечательный журнал Химия и жизнь).
На самом деле, кроме поиска закономерностей, метод выполняет еще одну задачу: отделяет существенные данные от несущественных; и кроме этого обладает еще одним важным свойством, о котором я скажу в конце. Применив этот метод, мы наконец узнаем, каков на самом деле был кратчайший маршрут дедушки Ляо и что считать его действительным направлением движения, а что — отклонениями (эх, дедушка Ляо, если бы ты меньше просиживал в кабачке то не пришлось бы связываться с отклонениями!).
Мы неспроста тренировались на собственных векторах и числах, поскольку они являются основой для реализации метода PCA (есть и другие реализации). Если мы поняли это, то до понимания реализации метода остался только один шаг. Этот шаг — использование матрицы линейного преобразования как ковариационной матрицы выходных данных.
Итак, начнем с выборки следов дедушки Ляо, которую для солидности будем именовать треком из 10 точек:
|
1 2 3 |
track = [[ 2.4 0.7 2.9 2.2 3. 2.7 1.6 1.1 1.6 0.9] [ 2.5 0.5 2.2 1.9 3.1 2.3 2. 1. 1.5 1.1]] |
Уберем из трека постоянную составляющую и найдем ковариационную матрицу трека:
|
1 2 3 |
np.cov(track) = [[ 0.717 0.615] [ 0.615 0.617]] |
Сделаем передышку и осмыслим сделанное (физический смысл — основа любого метода). О чем говорит ковариацонная матрица? Одинаковые значения 0.615 говорят о степени связи (корреляции) переменных x[0..9] и y[0..9], которые являются соответствующими координатами трека (простите, в Питоне индексы начинаются с нуля). Элементы главной диагонали 0.717 и 0.617 говорят о корреляции этих переменных с собой же, то есть это практически значения мощности, если переменные интерпретировать как сигналы.
Поэкспериментируем с ковариационной матрицей на более простых данных. Будем брать значение ковариации слегка зашумленных отрезков из трех точек.
Диагональный отрезок под 45°:
|
1 2 3 |
np.cov([1,1.9,3.1],[0.9,2.1,2.9]) array([[ 1.11, 1.04], [ 1.04, 1.01]]) |
Диагональный отрезок под -45°:
|
1 2 3 |
np.cov([1,1.9,3.1],[-0.9,-2.1,-2.9]) array([[ 1.11, -1.04], [-1.04, 1.01]]) |
Вертикальный отрезок:
|
1 2 3 |
np.cov([0,-0.1,0.1],[0.9,2.1,2.9]) array([[ 0.01, 0.04], [ 0.04, 1.01]]) |
Горизонтальный отрезок:
|
1 2 3 |
np.cov([0.9,2.1,2.9],[0,-0.1,0.1]) array([[ 1.01, 0.04], [ 0.04, 0.01]]) |
Как видно по результатам, ковариационная матрица чувствительна к углу поворота отрезка. Она определяет степень разброса данных и их ориентацию в пространстве. Теперь, основываясь на этой матрице, было бы хорошо найти вектор, который смотрит в сторону наибольшего разброса. Этот вектор на самом деле тот самый компонент метода PCA, который нам нужен.
Если мы еще раз нырнем в теорию, то обнаружим, что искомые векторы на самом деле являются собственными векторами ковариационной матрицы.
Итак, за работу!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# следы дедушки Ляо на двумерной плоскости - трек track = np.array([ [2.4,0.7,2.9,2.2,3.0,2.7,1.6,1.1,1.6,0.9], [2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1] ]) # убираем постоянную составляющую, или среднее значение A = track.T M = (A-np.mean(A.T,axis=1)).T # находим собственные числа и векторы ковариационной матрицы [evalue,evector] = np.linalg.eig(np.cov(M)) # а это уже что-то новое rotated_track = np.dot(evector.T,M) |
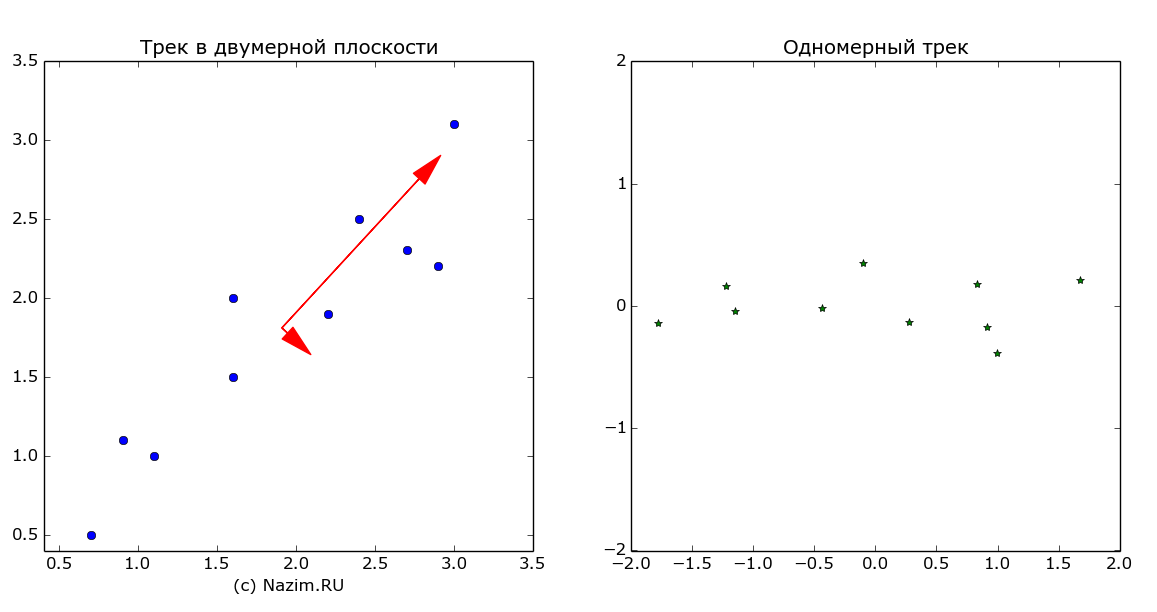
Осталось запечатлеть результат работы на картинке. Красным цветом представлены собственные векторы ковариационной матрицы, которые и есть главные компоненты, или оси максимальной изменчивости данных.
На картинке справа — тот же самый трек в новой системе координат, или проще говоря повернутый на угол одной из осей главных компонент (еще одна причина того, для чего ее нужно было искать). Такое преобразование выполняет последняя строка фрагмента программы:
|
1 |
rotated_track = np.dot(evector.T,M) |
Кажется, подошло время к тому, чтобы сделать кое-какие выводы.
Тайное становится явным
«Человек, у которого только одни часы, точно знает который час. Обладатель двух часов ни в чем не уверен»
До сих пор все шло прекрасно. Ведь согласитесь, что мы в глубине души ожидали, что метод главных компонент подтвердит нашу не очень глубокую догадку о том, что трек дедушки Ляо проходит по оси юго-запад — северо восток. Так оно и есть. Но есть и вторая компонента, которая упрямо доказывает нам, что дедушка Ляо вполне мог двигать и по оси северо-запад — юго восток. И действительно, если ассортимент кабачка оказался забористым, герой нашего рассказа продвигался очень медленно, зато качало его из стороны в сторону будь здоров. Конечно, коротенький второй вектор говорит о том, что это направление как-бы не главное, но оно есть.
Теперь дальше. Мы действительно выделили закономерность во входном треке. Можем даже предположить, что главная компонента это и есть трек, искаженный шумом. Таким образом, мы разделили существенные и несущественные данные. И самое интересное, мы переместили трек в новую систему координат, вследствие чего он стал одномерным (говоря по научному, мы выполнили ортогонализацию). Понижение размерности входных данных — это большое достижение, например, для этого предназначены такие сложные итерационные методы, как преобразование Грама — Шмидта.
И в конце вишенка на торте. Посчитаем ковариационную матрицу повернутого трека:
|
1 2 3 |
np.cov(rotated_track) [[ 1.284e+00 -4.009e-17] [ -4.009e-17 4.908e-02]] |
Если считать очень-очень маленькие числа (в степени -17) нулями, то ковариационная матрица нового трека
|
1 2 |
[[ 1.284 0] [ 0 4.908e-02]] |
стала диагональной! А это значит, что корреляция, а именно взаимозависимость между координатами x и y исчезла. Более того, малое значение корреляции для координаты y говорит о том, что мы имеем дело с шумом малой мощности. Сказанное влечет за собой важное следствие: теперь мы можем анализировать трек только по одной новой координате x, не обращая внимания на другую: она в силу ортогональности системы не оказывает никакого влияния.
Вернемся еще раз к собственным векторам. При программировании метода главных компонент, вычислительная сложность падает именно на алгоритм нахождения этих векторов. Это нужно учитывать при реализации, чтобы не получить проблемы с быстродействием системы.
Всем большой привет от дедушки Ляо!
Updated, или как все это было посчитано
Из комментариев стало ясно, что нужно заполнить пробелы этой статьи — более подробно рассказать, как были получены данные. Поэтому даю фрагмент псевдокода Python, из которого все должно быть ясно:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# исходный трек track = np.array([ [2.4,0.7,2.9,2.2,3.0,2.7,1.6,1.1,1.6,0.9], [2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1] ] # убираем смещение из трека A = track.T M = (A-np.mean(A.T,axis=1)).T # находим собственные числа и векторы [evalue,evector] = np.linalg.eig(np.cov(M)) # готовим собственные векторы для отрисовки m = np.mean(track,axis=1) r0 = evector.T*evalue r = r0.T # в левом окне: # рисуем собственные векторы с учетом смещения ax.arrow(m[0], m[1], -r[0,1], r[0,0]) ax.arrow(m[0], m[1], r[1,1], -r[1,0]) # также рисуем наш трек ax.plot(track[0,:],track[1,:]) # в правом окне: # рисуем трек в новом базисе score = np.dot(evector.T,M) plt.plot(score[0,:],score[1,:]) |
Картинку тоже подредактировал, теперь она в правильном масштабе

«Остановившиеся часы дважды в сутки показывают сверхточное время».
Спасибо за интересную идею — мне может пригодится для расчета вектора направления по РЛИ-данным, я так думал просто разные «средние» использовать.
Да, это пригодится.
В РЛ (или в КСА точно) может быть своя трекинговая обработка, которая строит траекторию и предсказывает будущее направление движения цели.
В документации по КСА не найдешь описаний используемых алгоритмов, не ясно как они даже переводят азимут/дальность в гео-местоположение на плоскости — может и Пифагором простым.
Там обычная геометрия, единственное в GPS и Глонасс используются разные модели поверхности Земли, необходимо делать перерасчет. По крайней мере раньше так было, точно не знаю как сейчас. Проекция цели на поверхность и координаты есть.
Дальше для экстраполяции используют фильтр Калмана. Построение трека проблем не представляет, поскольку основные источники наблюдения содержат информацию о борте. Вот с первичными локаторами выделение трека это искусство.
Можно присоседиться на поток данных с локатора и поиграться со своим трекером. Глядишь, там и новая КСА УВД появится )
Там геометрия сильно разная бывает, точно знаю два типа перевода азимута-дальности в гео. координаты. Какая модель использована для размещения сферы зоны на 20
монитора вообще непонятно. Темный лес — разработчик ничего не будет раскрывать. У нас так после ТО на локаторе в конфигурационный файл КСА попало значение оборота локатора в 5 сек., все самолеты вполне себе далеко за сверхзвук выходили, т.е. текущее значение оборота антенны даже не использовалось, тупо бралось то, что было в конфигурационном файле.P.S. Пробую треки строить — но сильно лютая мат.статистика для меня ;-). Может быть пока.
Вот как развертку сделать на плоский экран монитора — эта мысль мне вообще не приходила в голову, а ведь на самом деле там должна быть правильная проекция )
Получается в локаторе отметки времени шли не в зависимости от датчика поворота антенны, а по таймеру… это косяк разработчика
С треками хорошо будет работать в связке Python + numpy. Вся нужная математика и простая работа с массивами, плюс простое отображение данных.
Есть модуль фильтра Калмана, вся программа будет 3 — 4 строчки.
Думается на небольших расстояниях там разница небольшая — «сова на глобус» вполне натянется. Но сам факт скрытия алгоритмов обработки разработчиком несколько напрягает.
Здравствуйте. Из всех материалов, которые мне удалось найти, пока я пыталась познать PCA, этот наиболее логичный и понятный, спасибо Вам большое 🙂
Единственная проблема, которую не удалось решить и воспроизведением ваших действий, и понять из любых других мануалов — как из собственных чисел и векторов матрицы вы получаете те векторы — оси эллипса разброса значений на рисунке?
Переход от
# находим собственные числа и векторы ковариационной матрицы
[evalue,evector] = np.linalg.eig(np.cov(M))
к
Красным цветом представлены собственные векторы ковариационной матрицы, которые и есть главные компоненты, или оси максимальной изменчивости данных.
как-то затерялся.
По вашему примеру:
track = np.array([[2.4, 0.7, 2.9, 2.2, 3.0, 2.7, 1.6, 1.1, 1.6, 0.9],
[2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1]])
A = track.T
M = (A — np.mean(A.T, axis=1)).T
print np.cov(M)
[evalue, evector] = np.linalg.eig(np.cov(M))
print(‘Eigenvectors \n%s’ % evector)
print(‘Eigenvalues \n%s’ % evalue)
Я получаю:
Cov matrix
[[0.71655556 0.61544444]
[0.61544444 0.61655556]]
Eigenvectors
[[ 0.73517866 -0.6778734 ]
[ 0.6778734 0.73517866]]
Eigenvalues
[1.28402771 0.0490834 ]
Да, вы правы, перехода не прослеживается )
Причина в том что красные стрелки нарисованы в неправильном масштабе. Должно быть так:
mean=np.mean(A.T,axis=1)
array([ 1.91, 1.81])
mean+evector*evalue
array([[ 2.85398977, 1.77672767],
[ 2.78040823, 1.84608507]])
Последнее есть настоящие координаты концов красных стрелок, а начало соответствует смещению mean, которое мы вычли для вычисления ковариационной матрицы, а теперь надо поставить начало векторов на место.
Спасибо за замечание, позже дополню статью )
То есть так? И уже с учетом длины векторов?
pc1 = ([1.91, 1.81][ 2.85398977, 1.77672767])
pc2 = ([2.85398977, 1.77672767][ 2.78040823, 1.84608507])
Тогда что-то не сходится… — https://cdn1.savepice.ru/uploads/2018/4/25/da5a0b684deb7acb79c1df38280c1bf2-full.png (график, не нашла как загружать картинки сюда)
Если в массиве
mean+evector*evalue
([[ 2.85398977, 1.77672767],
[ 2.78040823, 1.84608507]])
значения распределены как
([[x_pc1, y_pc1][x_pc2, y_pc2]])
Если же
([[x_pc1, x_pc2][y_pc1, y_pc2]]), то уже больше похоже на правду — https://cdn1.savepice.ru/uploads/2018/4/25/6987a7935a5418c7f0b84d1e8ad27f13-full.png
Но векторы не ортогональны. И меньший совершенно не поход на то, что изображено у вас.
Спасите)))
p.s. должно быть так, криво скопировала:
То есть так? И уже с учетом длины векторов?
pc1 = ([x0 = 1.91, y0 = 1.81][x1 = 2.85398977, y1 = 1.77672767])
pc2 = ([x0 = 1.91, y0 = 1.81][x2 = 2.78040823, y2 = 1.84608507])
Да, все так и есть. Мы называем красные стрелки векторами в геометрическом смысле, не в алгебраическом, т.е. эти векторы имеют координаты начала и конца. Координаты начала у обоих стрелок одинаковые — это mean, а координаты конца соответствуют
mean+evector*evalue
array([[ 2.85398977, 1.77672767],
[ 2.78040823, 1.84608507]])
При v = evector*evalue
Первый вектор:
v[:,0]
Второй вектор:
v[:,1]
Ортогональность проверяем в алгебраическом смысле, т.е.
np.dot(v[:,0],v[:,1])
6.9388939039072284e-18
практически равно нулю, значит векторы-стрелки ортогональны
То есть между векторами не должно быть четко 90°? Вот это в статьях которые я читала было неочевидно 🙁
p.s. по логике видно, но чтобы вот точно на всякий случай для закрепления:
Eigenvectors
[[ 0.73517866 -0.6778734 ]
[ 0.6778734 0.73517866]]
это Eigenvectors
[[ x1 x2 ]
[ y1 y2]]
а Eigenvalues
[1.28402771 0.0490834 ]
это
[length(pc1) length(pc2)]?
И не очень поняла, что имелось в виду здесь?
Первый вектор:
v[:,0]
Второй вектор:
v[:,1]
Дабы не флудить тут, могу предложить Вам перейти на почту/вк, если так будет удобнее.
А по попыткам воспроизведения также меня смущает:
1. В Вашем примере, если мой график https://cdn1.savepice.ru/uploads/2018/4/25/6987a7935a5418c7f0b84d1e8ad27f13-full.png верен, вторая компонента получается довольно-таки короткой для покрытия данного эллипса наблюдений. Нормально ли это?
2. На моей выборке в принципе получается ерунда:
def PCA(X, meter1, meter2):
A = X[[meter1, meter2]]
print A
X_std = (A — np.mean(A.T, axis=1)).T
print(‘Standardizing matrix\n%s’ % X_std)
cov_mat = np.cov(X_std)
print(‘Covariance matrix\n%s’ % cov_mat)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
# ([[x_pc1, x_pc2][y_pc1, y_pc2]])
print(‘Eigenvectors \n%s’ % eig_vecs)
print(‘Eigenvalues \n%s’ % eig_vals)
for ev in eig_vecs:
np.testing.assert_array_almost_equal(1.0, np.linalg.norm(ev))
print(‘Eigenvalues*Eigenvectors \n%s’ % (eig_vals*eig_vecs))
return eig_vals*eig_vecs
Изображение (https://yadi.sk/i/JA3xbBCF3UnMSa да, они почти в одной точке)
Вывод:
GarageMudroomLights [kW] DiningRoomOutlets [kW]
0 0.004261 0.001795
1 0.004264 0.001789
2 0.004256 0.001796
3 0.004269 0.001763
4 0.004241 0.001687
5 0.004240 0.001709
6 0.004254 0.001694
7 0.004211 0.001700
… … …
5192 0.005356 0.002340
5193 0.021194 0.001927
5194 0.004367 0.001843
5195 0.004385 0.001847
5196 0.004416 0.001801
5197 0.004404 0.001804
5198 0.004406 0.001798
[5199 rows x 2 columns]
Standardizing matrix
0 1 2 3 4 \
GarageMudroomLights [kW] -0.004204 -0.004200 -0.004209 -0.004195 -0.004224
DiningRoomOutlets [kW] -0.000950 -0.000956 -0.000949 -0.000982 -0.001059
5 6 7 8 9 \
GarageMudroomLights [kW] -0.004225 -0.004210 -0.004254 0.023169 0.023314
DiningRoomOutlets [kW] -0.001036 -0.001051 -0.001045 -0.001029 -0.000454
… 5189 5190 5191 5192 \
GarageMudroomLights [kW] … 0.005363 0.023668 0.006716 -0.003109
DiningRoomOutlets [kW] … -0.000985 -0.000830 -0.000655 -0.000405
5193 5194 5195 5196 5197 \
GarageMudroomLights [kW] 0.012729 -0.004098 -0.004080 -0.004049 -0.004060
DiningRoomOutlets [kW] -0.000818 -0.000903 -0.000899 -0.000944 -0.000941
5198
GarageMudroomLights [kW] -0.004059
DiningRoomOutlets [kW] -0.000948
[2 rows x 5199 columns]
Covariance matrix
[[1.18487483e-04 1.26216746e-05]
[1.26216746e-05 4.87727130e-04]]
Eigenvectors
[[-0.99941764 -0.03412315]
[ 0.03412315 -0.99941764]]
Eigenvalues
[0.00011806 0.00048816]
Eigenvalues*Eigenvectors
[[-1.17987789e-04 -1.66574900e-05]
[ 4.02846079e-06 -4.87873786e-04]]
В итоге значения, да и eigenvalues выходят довольно-таки маленькие.
Можете ли Вы подсказать что не так? 🙁
При стандартизации матрицы так, кстати, результат другой:
X_std = StandardScaler().fit_transform(A)
print(‘Standardizing matrix\n%s’ % X_std)
cov_mat = np.cov(X_std, rowvar=False)
Изображение (https://yadi.sk/i/cDy4znJL3UnMPE). И даже если тут выглядит приличнее, чем при стандартизации только путём вычитания среднего, то всё равно видно, что главные компоненты располагаются отнюдь не так.
Standardizing matrix
[[-0.38623409 -0.04303795]
[-0.38592786 -0.04328956]
[-0.38674447 -0.04298764]
…
[-0.3719932 -0.04276122]
[-0.37306512 -0.04261028]
[-0.37296296 -0.04291215]]
Covariance matrix
[[1.00019238 0.05251409]
[0.05251409 1.00019238]]
Eigenvectors
[[ 0.70710678 -0.70710678]
[ 0.70710678 0.70710678]]
Eigenvalues
[1.05270647 0.94767829]
Eigenvalues*Eigenvectors
[[ 0.74437588 -0.67010975]
[ 0.74437588 0.67010975]]
В чём же разница между стандартизациями, почему выходят разные векторы и как понять что подходит?
Добавил апдейт статьи, привел формулы как все было посчитано. Картинку тоже обновил.
Давайте комменты по новой версии )
Огромное спасибо за статью! Сейчас приходиться анализировать возможности (реальные) Singular Spectrum Analysis, Ваш материал значительно упростил понимание идеи метода.
Спасибо за оценку работы! Старался говорить доступным языком )
Я честно говоря чуть не заплакал, когда прочитал. Давно искал человеческим языком написанный материал по данной теме. Спасибо, супер.